実のところ、統計はかなり苦手で、学生時代は極力避けてきましたが、ビッグデータと向き合うにつれて避けては通れない付き合いになって参りました。
正直に申し上げてまだまだわからない点が沢山ありますが、実データを相手に実際の現象に向き合うことで自分の理解が深められたように感じています。
さて、ここでは航空機の着陸時の接地点:タッチダウンポイントの統計を紹介します。筆者が富士山静岡空港で着陸した際のスレッシュホールドから接地点までの距離の統計です。
なお、このデータは旅客機に搭載されている記録装置から抽出したもので、筆者以外の機長のデータは含まれておりません。(筆者の監督下で副操縦士が操縦したデータは含まれます)
また、所属していた(株)フジドリームエアラインズ様の許可を得た上での掲載となっております。航空の発展のために快く許可をして頂いた事に感謝申し上げます。
通常、着陸する際にはある一点をめがけて進入し、スレッシュホールドを少し過ぎてからフレア操作を行い、めがけた点よりやや遠い地点に接地します。
目標にするある一点は、悪天候を除いてほとんどの場合は同じ場所です。
従いまして、理想的には常に同じ点を目標にして進入し、それより遠くのある一点に常に接地できればしめたものですが、実際はそうはいきません。
何事も同じですが、常にばらつきが生じます。
接地点も当然ばらつきます。
お客様として飛行機に乗られていた場合、経験すると思いますが、ある時は着陸寸前に滑走路のすぐ上です~っと延びたり、ある時はそうで無かったりします。
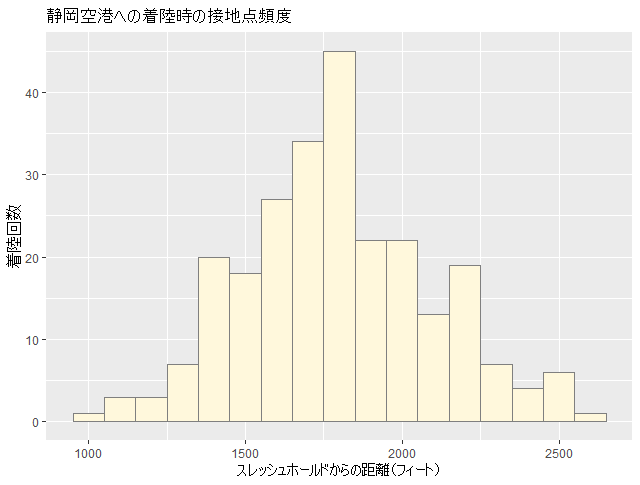
180回分の着陸データからばらつきの度合いを示したのが下記のヒストグラムです。
長方形の幅は100フィートですので、1800フィート付近に最も多く接地していることがわかります。
そしてショートランディング気味の時は1000フィート、ロング気味は3000フィートとなっています。
上記の3つの地点がどの辺か?ということでGoogleEarthの衛星画像上にマークしてみました。

画像は、富士山静岡空港の滑走路30(以下FSZ30と略します)を真上から眺めたものに筆者の接地点の範囲をピンでマークしたものです。また、筆者がフレア操作を開始するまでにめがけている地点を「最初にめがける地点」としてマークしました。
実は富士山静岡空港のように比較的長い滑走路では、1700~1800フィート前後で接地するように着陸してきたつもりですが、先ほど紹介したグラフをはじめて描いたときは正直申し上げて、驚きました。
「つもり」が「本当」になっていたわけです。
滑走路上に黒く見えるのは全てのパイロットが接地の時につけたタイヤ痕でして、筆者の接地点の統計と良く一致しています。また仮に他のパイロットの統計を計算するとおそらく同じような結果になっていると思われます。
もし、達人パイロットのデータを見ることが出来たとすると、どうなっているのでしょうか?
達人は毎回毎回狙った地点に接地していることでしょう。
そうするとグラフの形は、私のようになだらかな山では無く、尖った山の形をしているに違いありません。
なお、なだらかな山は正規分布と言えそうです。
ちなみに正規分布の直感的な理解は次のyoutubeをご覧頂くとわかります。
今後徐々に色々なテーマ、データサイエンスと航空機運航の接点について分かり易く紹介するつもりです。
さて、以下から急に専門的な記述になりますが、データサイエンスに興味のある方は是非おつきあいください。
統計をご存じの方でしたら、先ほどのヒストグラムは何となく正規分布に似ているかな?と感じられると思われた方が多かったと思います。
もしそうであったら面白い発見です。
確かめるために最初にQ-Qプロットを描いてみました
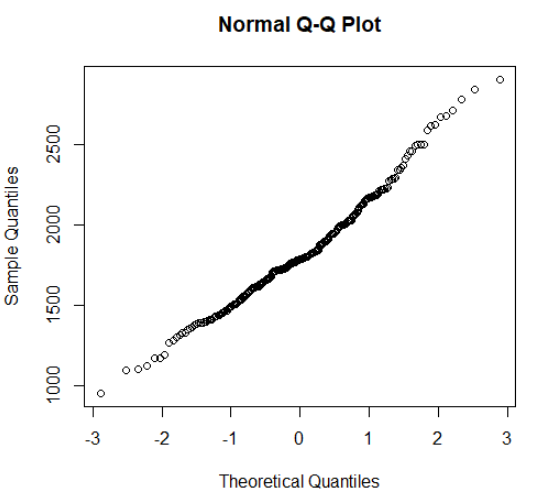
左図はQ-Qプロットです。
概ね直線上に並んでいます。
なんとなくいい感じですので、正規分布に従うか否かをコルモゴロフ・スミルノフ検定を行ってみました。(筆者が使っているプログラミング言語はRです)
しかし結果は
p-value = 0.02841
となって有意水準が5%で帰無仮説 (H0) :標本分布が正規分布に従うことが棄却され、残念な結果になりました。
もし正規分布である事がわかれば今後の解析の応用範囲が一気に広がります。
少し心が折れそうになったのですが、着陸の状況を振り返ってみると一つひらめきました。
正規分布に従う着陸状況と、そうではない(厳しい気象条件下の)着陸状況の結果が混在しているのでは無いか?
厳しい気象条件とは具体的にはガストを伴ったような強い風が吹き荒れる日です。
こういう状況では、接地点が延び気味になってしまいます。
経験上おおよそ2600フィート以上の時がそれに該当します。
そこで先ほどのヒストグラムをよくよく見ますと、丁度2600フィート以上の接地点が正規分布らしからぬ形になっているようです。
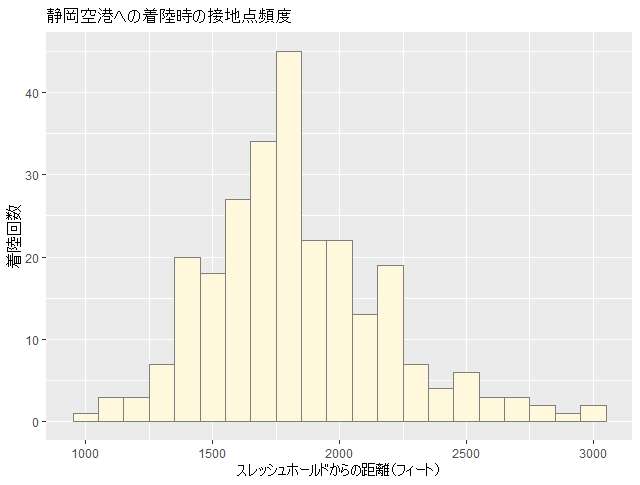
そこで、大胆ですが2600フィート以上のデータをカットして、再び検定にかけました。
左がカット前、右がカット後で、なんとなくいい形になっています。
早速検定にかけますと、
p-value = 0.2723
となり、帰無仮説 (H0) :標本分布が正規分布に従うことが保留されました。
これから類推されることは、気象条件が厳しくない時の接地点の距離はおそらく正規分布に従い(正確にはデータの分布が正規分布と一致しているかどうかは何とも言えないのですが)、厳しいときは外れ値となって現れてくるのではないかということです。
航空機の安全運航の観点からはこの外れ値が出来るだけ小さく、頻度が少ないことが望まれます。
又、今回は筆者の経験から2600フィート以上という閾値で外れ値を推定しましたが、簡単なプログラムを組むことで、検定を繰り返して閾値の限界を探ることが出来ます。
この手法は他の滑走路にも応用出来ます。
つまり他の短めの滑走路で、何フィート以上延びてしまったら、「普通の着陸とは異なる接地点でした」と合理的に言えるのではないかと思います。
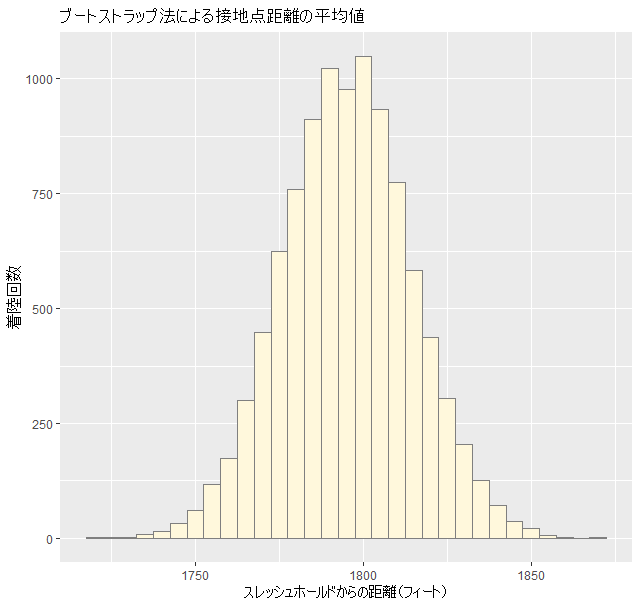
最後に、2600フィート以上のデータをカットしたものを正規分布であると仮定して、ブートストラップ法で接地点の平均値を求めてみました。
正規分布であると仮定できると応用範囲が広まります。
重複を許して1万回(通常は千回で充分とのことですが)サンプリングを行い、ブートストラップ法で平均値を出した結果が左図。
標本データが属する母集団(筆者と副操縦士が静岡空港で行った接地点のスレッシュホールドからの距離)のデータ平均値は、信頼区間95%で1758フィートから 1833フィートにあると言えそうであることがわかりました。
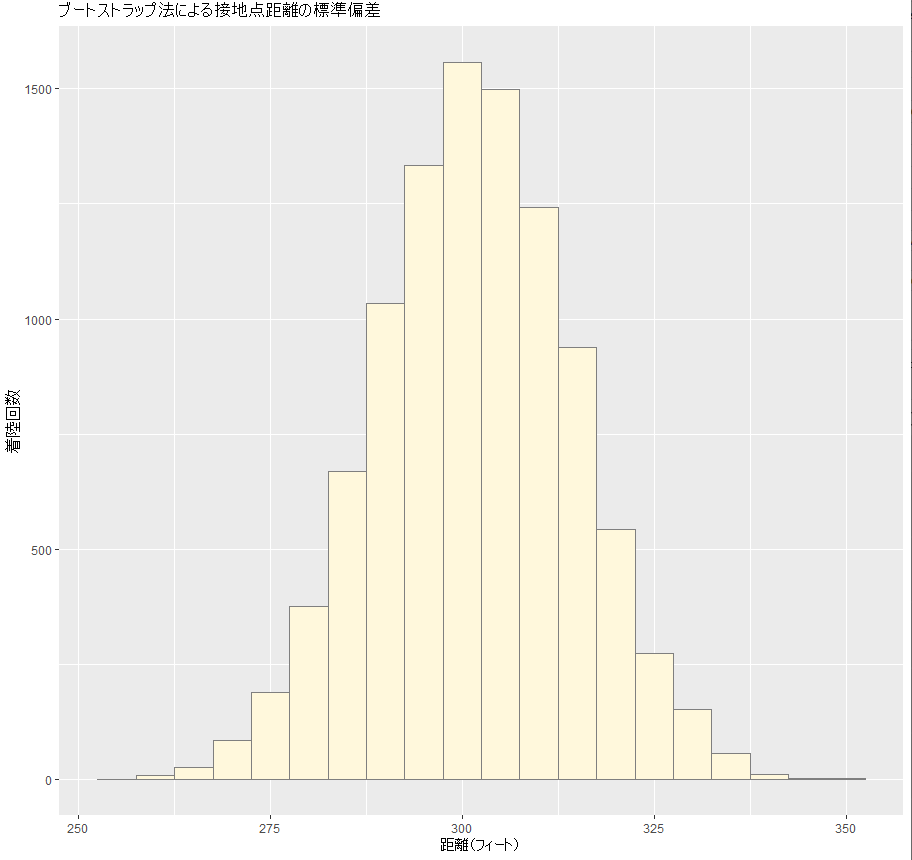
勢いに乗って、同様の手法で標準偏差を出してみます。
標準偏差を出すと接地点の範囲がわかります。
標準偏差:σは信頼区間95%で276フィートから327フィートである事がわかりました。
平均±2σの間には95%のデータが入ることからこのデータの接地点に付いては以下のように言えそうです。
おおよそ接地点の平均は1758フィートから 1833フィートにあり、その地点±552~654フィートの区間に95%の確率で接地する。
分かり易く大まかに書いてしまいますと、普通のランディングであれば、1100フィートから2500フィートの範囲に95%の確率で接地できるといった感じになります。
このように航空機運航とデータサイエンスは大きな関連性を持つ予感がします。
今後色々と紹介したいと思います。