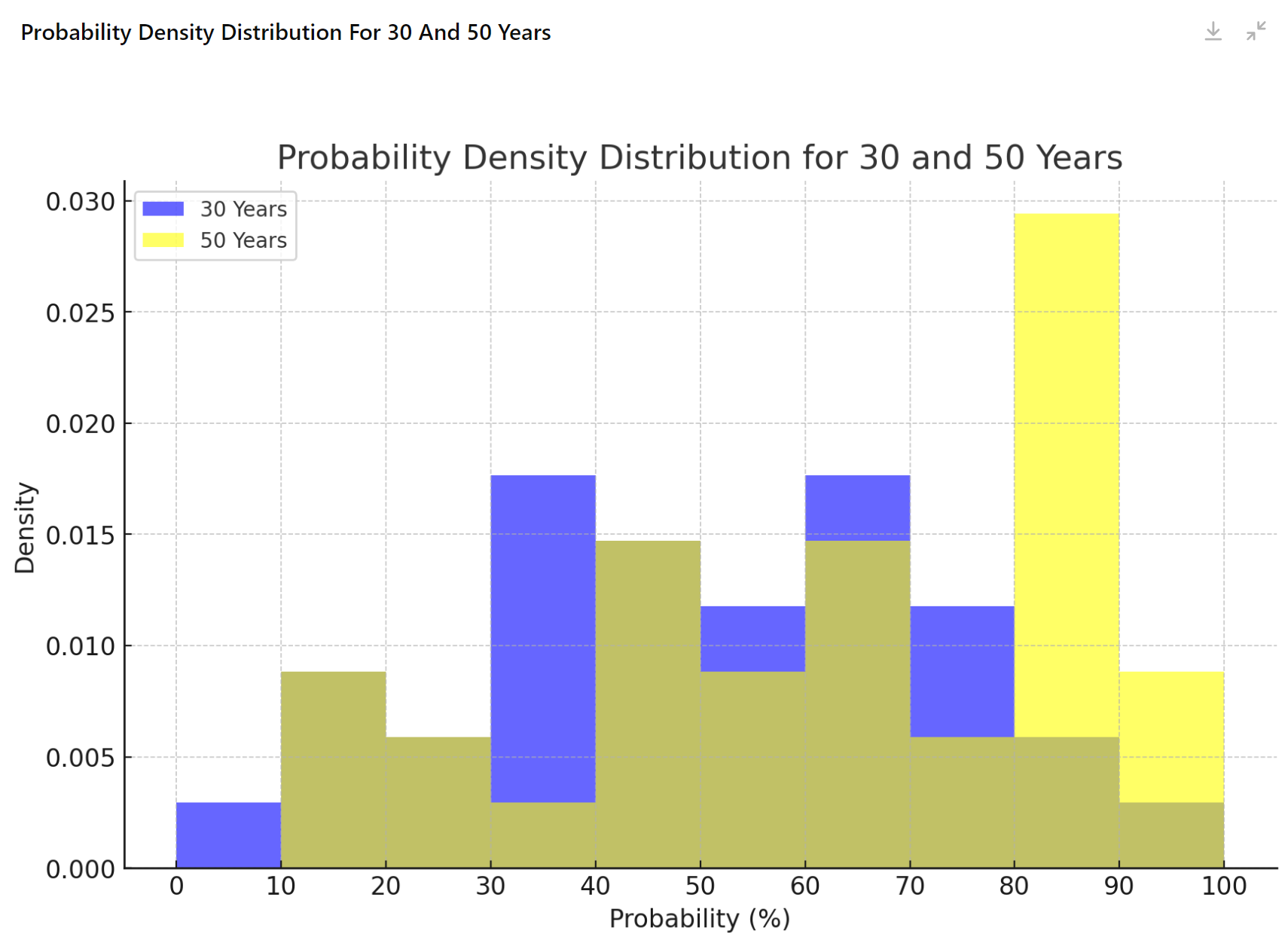
実はここまで活用してきた信念を示すオレンジと青のグラフは、分かり易くするために使ってきましたが、そろそろ本当のグラフを紹介したいと思います。
本当のグラフとは確率密度分布と呼ばれます。

ただし、聞き慣れないこのグラフ、理解が困難です。そこで、天気予報とコイン投げという身近な話題から始めて徐々に解説いたしましょう。

テレビを見ていたら「明日の〇〇地方の降水確率は50％です」と報じられていたとしましょう。
ここで考えてみて下さい。
この予報を判断した人は「明日の〇〇地方の降水確率は50％である」事を100％の確率で起こりうると考えたでしょうか？（自信満々で考えたのでしょうか？）
％が2つ出てきて混乱するかもしれませんが、今回は「確率の確率」が大きなテーマになります。

ひょっとすると間違いなく100％の確率で起こると判断したかもしれませんし、60％の確率（ひょっとすると違うかもしれない）で起こると判断したかもしれません。
斜めのフォントで書いた2つめの％は信念の度合いと考えて良いと思います。

別の例を引き合いに出しましょう。
何かを決めるときにコイン投げをすることがあると思います。

種も仕掛けもないと完全に信じ切ることが出来るコインを、何回か投げた後に次に出る裏表を予想してみましょう。
この場合「次に表が出る確率は50％である」という予想は「100％正しい」と言い切れると思います。


しかし、種も仕掛けもありそうな、見るからに怪しげなコインを、例えば10回投げて10回連続で裏が出たとしましょう。
怪しさはとてつもなく感じられます。

裏裏裏裏裏裏裏裏裏裏→次に表が出る確率は？

この時、「次に表が出る確率は50％である」という予想は100％正しいと言い切れるものでしょうか？
おそらく100％ではなく、それより低い値であると思います。
それでは、表が出る確率を色々想定して考えてみましょう。（下記は分かり易く10％刻みにしていまして、実は数学的にはおかしな説明ですがご容赦ください）

次は表がでる確率は　100％と考えられる　　　0％
次は表がでる確率は　　90％と考えられる　　　0％
次は表がでる確率は　　80％と考えられる　　　0％
次は表がでる確率は　　70％と考えられる　　　0％
次は表がでる確率は　　60％と考えられる　　　0％
次は表がでる確率は　　50％と考えられる　　　5％
次は表がでる確率は　　40％と考えられる　　　10％
次は表がでる確率は　　30％と考えられる　　　15％
次は表がでる確率は　　20％と考えられる　　　20％
次は表がでる確率は　　10％と考えられる　　　30％　
次は表がでる確率は　　　0％と考えられる　　　20％

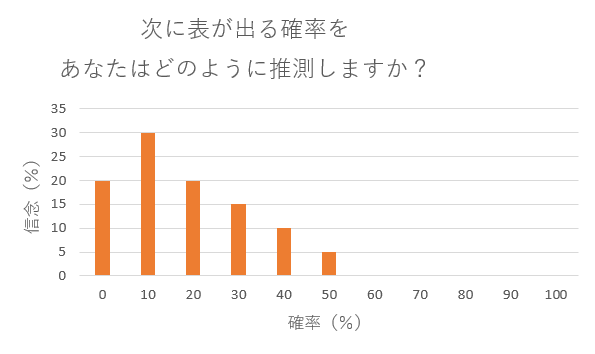
信念の％は私が適当に設定した値ですが、棒グラフで最も高いものは10％であって、この例では私の推測は
　10％の確率で表が出る　.. 最も有力
　0%または20%の確率で表が出る .. 次に有力
などの表現が出来ると思います。


読者によっては当然考え方も異なるためグラフの形は変わると思いますが、ここで強調したいのは、この手の悩ましい問題に対する判断は下のグラフのように「間違いなく10％です」のように断定的に考えるのは難いということです。

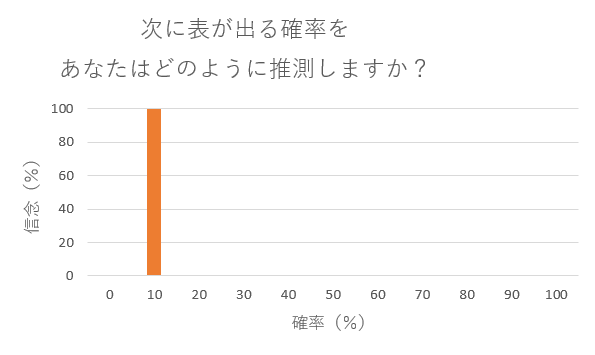
　このように考えてみると、図1のほうが、人間の頭の中をより現実的に表現していると考えられます。
図1からは、誰かに「次の表が出る確率は何％？」と聞かれて、一言で答える必要がある場合「10％」と答えると思います。
しかし、それだけではなく、どちらかというと20％～50％の確率も考えられるということも見えてきます。

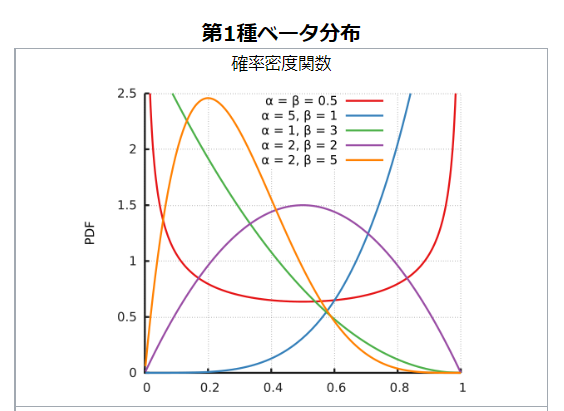
実は図1の山を滑らかにしたものが確率密度関数と呼ばれています。
関数には多くのものがあるのですが、その中の一つが、β（ベータ）分布と呼ばれています。
講釈は追々行いますが、このグラフ、慣れてしまうととても便利なのです。

確率密度関数やベータ分布は一旦脇に置いて、RTO（リジェクトテイクオフ：離陸中断）の話題に突入しましょう。
想定としては、離陸中に右エンジンから異音（ドーン）が発生し、振動（ガタガタ）が感じられて離陸を中断、完全停止をしてチェックリクストを行うというものです。

エアラインで訓練をしている方ならばわかると思いますが、この時行うべきチェックリクストには通常2～3種類あります。
今回は典型的な例としてそのうちの2種類を取り上げましょう。

1　エンジンが激しく壊れた時に行うチェックリスト
　　Engine Severe Damage Checklist
2　エンジンが異常燃焼した時に行うチェックリスト
　Engine Surge or Stall Checklist

事象の重大度は　1＞2　ですが、パイロットは上記のうちいずれかを判断して行うのです。

仮に、異音がものすごく大きく、振動もひどいものであったらチェックリストは1を行います。
しかし、悩ましい状況（異音は中くらい、振動も中くらい）だった場合はどうでしょうか？
一般の方が読んでいらっしゃったら、いつも1をやれば良いのではないか？と思われるかもしれませんが、1は消化剤をエンジン内部に噴射したり、根本からシャットダウンして再始動を不可能にする手順なので、実施するためには大きな決断が必要なのです。
この点がパイロットのつらいところですが、下記のグラフのように判断できるでしょうか？

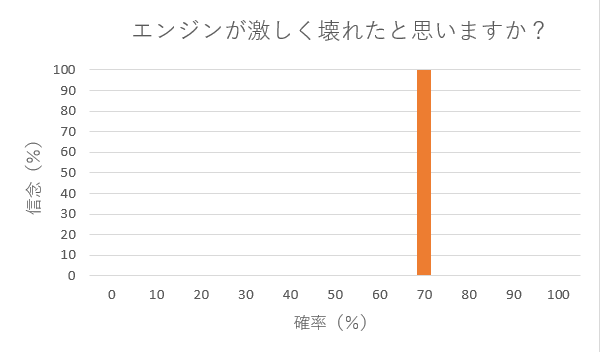
先ほどの表がでる確率を10％と断言したように、70％だと言い切れますか？

上記よりも次の方が心の中を表現しているのではないでしょうか？
「一言で言うと70％だが、それより多い確率で激しく壊れている可能性もありそうだ。また、激しく壊れていない確率も捨てきれない」

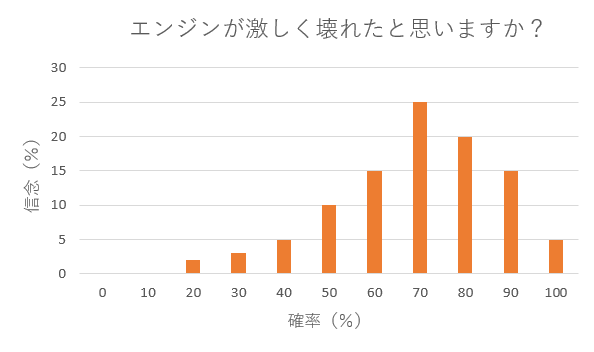
さて、ここからが本題です。
パイロットは1か2のいずれかのチェックリストを選ばなければなりませんが、70％（最も高いオレンジ色の棒の確率）という値を根拠に考えるべきでしょうか？
「一言で言うと70％だが、それより多い確率で激しく壊れている可能性もありそうだ。また、激しく壊れていない確率も捨てきれない」
という心の内を数値で表現するためにはどうすればいいのでしょうか。

このためには、例えば次のように考えると良いでしょう。
確率が50％以上であると考えている自分の信念
確率が50％未満であると考えている自分の信念
上記の比率は？

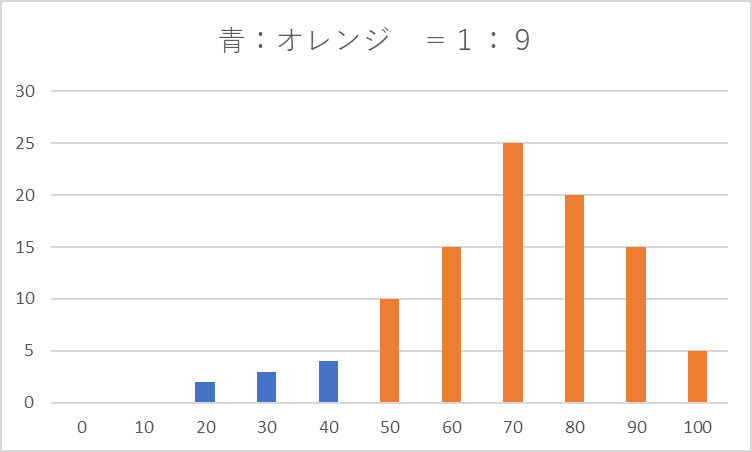
これはオレンジの棒の長さを足し合わせて比較する事によって求められます。
確率が50％未満の信念　：　確率が50％以上の信念　=　　
2＋3＋5　：　10＋15＋25＋20＋15＋5　=
10 : 90　＝
1 : 9
つまりエンジンが激しく壊れている確率が50％以上であるという信念は50％未満という信念より9倍強いと言えます。

では50％を境にするのではなく、80％を境に考えてみましょう。
確率が80％未満の信念 ：　 確率が80％以上の信念　＝　　
2＋3＋5＋10＋15＋25 ： 20＋15＋5　　＝
60 : 40 ＝
3 :2
つまりエンジンが激しく壊れている確率が80％以上であるという信念は80％未満という信念より2／3程度であると言えます。

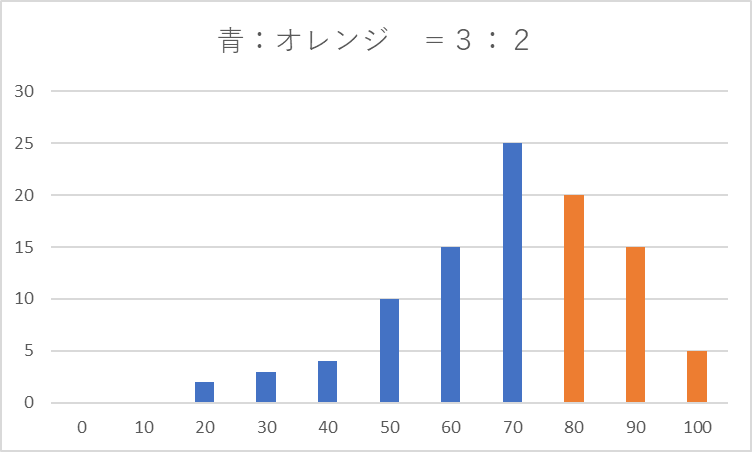
いかがでしょうか？
ちなみに筆者の心の中のグラフが仮にこの状況でしたら、激しく壊れていたと判断して、
1　エンジンが激しく壊れた時に行うチェックリスト：　
Engine Severe Damage Checklist　を行うべきであると考えます。

このように一旦、先ほどの棒グラフを描くことができれば、信念同士（激しく壊れている　VS　それほど激しくない）の比率で考えることが出来、判断がかなり楽になります。
この比率の考え方はオッズ比と呼ばれています。

パイロットは何かを決断するときに、色々考えると思いますが、そのプロセスとしてこの確率モデルのように考えているのかもしれません。

この章ではまだまだ語り足りない部分が沢山ありますので、次回以降紹介いたしましょう。